






Аэрогидродинамика — это наука о движении жидкостей и газов, которая занимается изучением проблем обтекания тел жидким или газообразным потоком и движения газов в пространстве, ограниченном стенками. Для моделирования процессов аэрогидродинамики на компьютерах и суперкомпьютерах автор статьи разработал мультиоператорный метод.
При численном моделировании физических процессов на электро-вычислительных машинах уравнения, которые описывают эти процессы, заменяются на алгебраические уравнения. Процесс их решения сводится к выполнению арифметических действий. Результаты вычислений — значения параметров изучаемых процессов в заданных точках исследуемой области. Записать алгебраические уравнения можно с помощью операторов. Оператор — это символические изображения математических операций, которые определяются формулами. Эти формулы указывают, какие арифметические действия нужно выполнить. Точность этих формул в конечном счете определяет точность получаемых решений. Математически точность характеризуется «порядками», которые показывают, как быстро убывают погрешности этих решений при увеличении числа заданных точек в области. При этом чем больше значения порядков, тем выше точность при фиксированном числе точек. Повышение точности численного моделирования является одним из приоритетных направлений современного развития вычислительной аэрогидродинамики.
Традиционные методы повышения порядков основаны на усложнении формул, определяющих операторы. Для реальных задач это может создавать определенные трудности и ограничения. В мультиоператорном методе повышение порядков достигается за счет использования комбинаций многих операторов, которые определяются одной и той же формулой очень простой структуры, но имеют разные значения некоторого параметра. Эти комбинации были названы мультиоператорами. При этом чем больше операторов, тем выше легко получаемые порядки. Построенные в последнее время мультиоператоры обеспечивают очень высокую точность численного моделирования. Более того, в результате оптимального выбора значений параметра применение мультиоператоров при численном моделировании физических процессов позволяет лучше «видеть» мелкие детали этих процессов в течение длительного времени их развития.
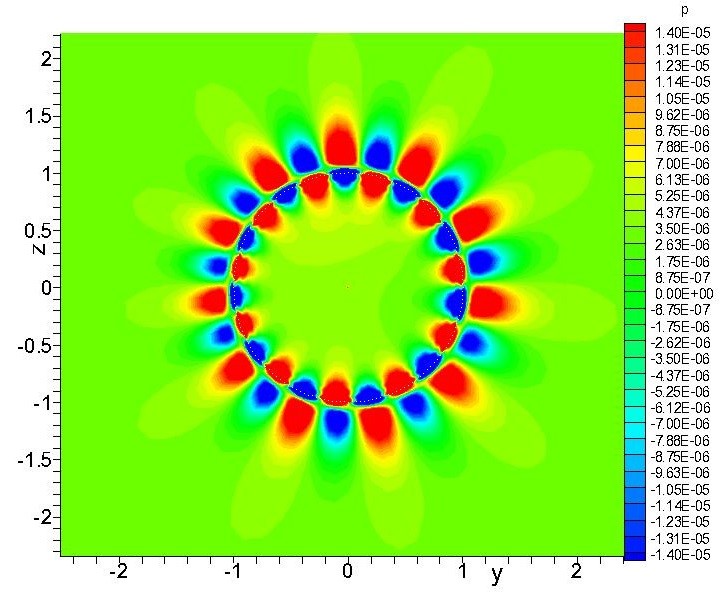
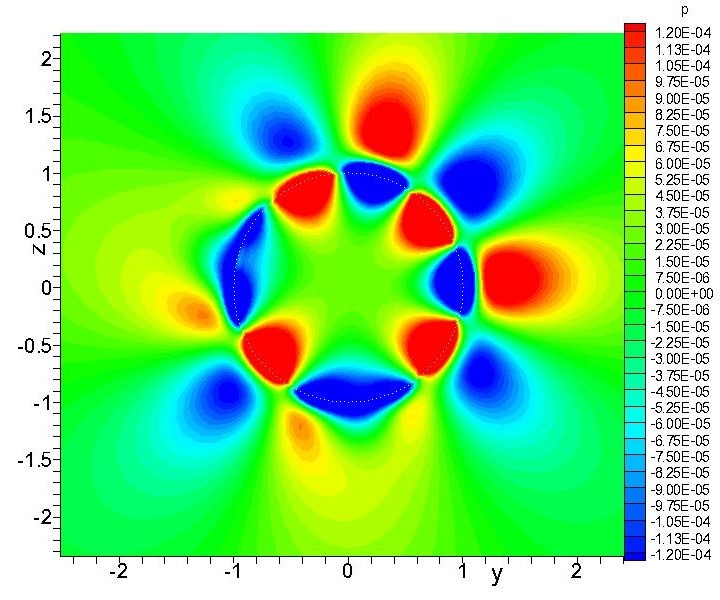
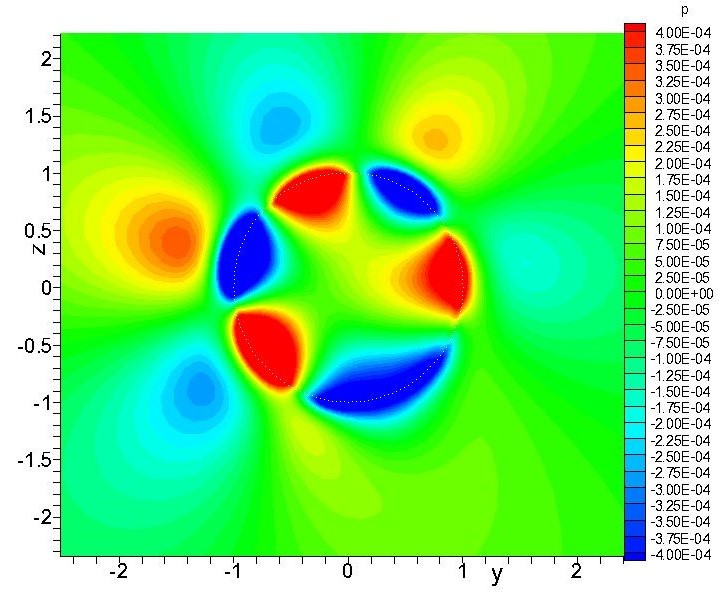
«Сущность работы состояла в развитии абсолютно новой вычислительной технологии — мультиоператорного метода. Применение мультиоператоров позволяет осуществлять численное моделирование различных физических процессов с точностью, намного превышающей точность существующих численных методов. Эта методика, не имеющая аналогов в нашей стране и за рубежом, была использована для решения задач аэрогидродинамики, для которых применение традиционных методов может оказаться недостаточно эффективным», — рассказал ведущий автор статьи Андрей Толстых, доктор физико-математических наук, заведующий отделом прикладной математической физики Вычислительного центра имени А.А. Дородницына Федерального исследовательского центра «Информатика и управление» РАН.
Автор отмечает, что разработанная методика имеет достаточно общий характер и может использоваться для решения различных классов задач, требующих точность вычислений, которая превосходит точность стандартных методов.
С помощью мультиоператорного метода ученые могут решать задачи аэроакустики, например, задачи снижения уровней шума от двигателей и обтекаемых элементов летательных аппаратов, задачи турбулентности, задачи численного моделирования гиперзвуковых течений. Еще мультиоператорные схемы высокой разрешающей способности могут использоваться при численном моделировании торнадо, а также других атмосферных явлений.
«Потребности в данной методике могут возникнуть в других областях, например, при численном моделировании климатических явлений, при численном исследовании процессов горения. В широком смысле наша цель состоит в создании инструмента, который может быть полезным для различных исследователей при решении их конкретных задач. В настоящее время работа продолжается, и мы рассчитываем на ее расширение», — заключил ученый.


